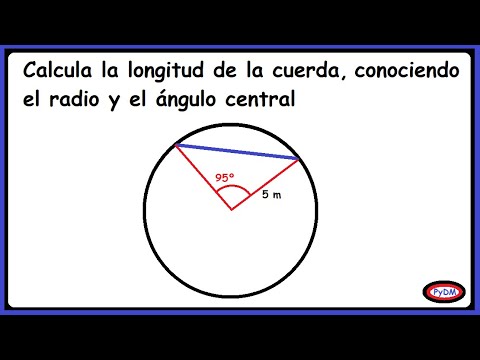
Cómo calcular la longitud de una cuerda de arco
Contenidos
Barrett escribió:Hola, me gustaría saber cómo calcular la cuerda de un arco de circunferencia conociendo la longitud del arco y el ángulo de la cuerda y una tangente.Gracias.¿Qué tangente? Si es una tangente a la circunferencia que pasa por uno de los extremos de la cuerda… hay que decirlo en el enunciado. :zen:
Black Jack escribió:¿Qué tangente? Si es una tangente al círculo que pasa por un extremo de la cuerda… tienes que decirlo en el enunciado. :zen:Es cierto, me disculpo. Efectivamente, es una tangente al círculo que pasa por uno de los extremos de la cuerda.
Corde d’un arc de cercle
{L=int _{J}|g'(t)|~mathrm {d} t=int _{J}\left||{frac {d}{dt}}(f\circ \theta )(t)\right|~mathrm {d} t=int _{J}||(f’circ \theta )(t)||\theta ‘(t)|~\mathrm {d} t=int _{I}||f'(s)|~\mathrm {d} s. }
{\a6}(t+mathrm {d} t)- f(t)|||approx |f'(t)\\Nmathrm {d} t\|={sqrt {\a la izquierda({\frac {mathrm {d} x}\a la derecha)^{2}+\a la izquierda({\frac {mathrm {d} y}\a la derecha)^{2}}mathrm {d} t. }
{L=int _{a}^{b} {cuadrado}(izquierda) de x} {mathrm {d}} {mathrm {d}} derecha)^{2}+izquierda de izquierda({frac {mathrm {d} y}{mathrm {d}t})^{2}+left({\frac {mathrm {d} z}{mathrm {d}t})^{2}}mathrm {d} t. }
L_{0}=int _{0}^{x_{0}} {{sqrt {1+{frac {9a^{2}}}x}};\mathrm {d} x={{frac {4}{9a^{2}}int _{0}^{{frac {9a^{2}}{4}x_{0}} {{sqrt {1+u}}; \mathrm {d} u={frac {8}{27a^{2}}left[(1+u)^{frac {3}{2}}right]_{0}^{{frac {9a^{2}{4}x_{0}={frac {(4+9a^{2}x_{0})^{frac {3}{2}-8}{27a^{2}}. }
{\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} \theta }}=a(1-\cos \theta ),\ {\frac {\mathrm {d} y}{\mathrm {d} \{\i}=a\i}sin \i} {\i}quad {\i}quad {\i}quad {\i}quad {\i}quad} izquierda({\frac {\mathrm {d} x}{\i}d} \i}derecha)^{2}+ izquierda({\frac {\mathrm {d} y}{\i}queda}{\i}derecha)^{2}=a^{2}(2- 2\cos(\theta ))=4a^{2} {left(1-\cos ^2}{frac {\theta }{2}\right)=4a^{2} {sin ^{2}{frac {\theta }{2}. }
Calcular la longitud de una cuerda de piano
{L=int _{J}|g'(t)|~mathrm {d} t=int _{J}\left||{frac {d}{dt}}(fcirc \theta )(t)\right|~mathrm {d} t=int _{J}||(f’circ \theta )(t)||\theta ‘(t)|~\mathrm {d} t=int _{I}||f'(s)|~\mathrm {d} s. }
{\a6}(t+mathrm {d} t)- f(t)|||approx |f'(t)\\Nmathrm {d} t\|={sqrt {\a la izquierda({\frac {mathrm {d} x}\a la derecha)^{2}+\a la izquierda({\frac {mathrm {d} y}\a la derecha)^{2}}mathrm {d} t. }
{L=int _{a}^{b} {cuadrado}(izquierda) de x} {mathrm {d}} {mathrm {d}} derecha)^{2}+izquierda de izquierda({frac {mathrm {d} y}{mathrm {d}t})^{2}+left({\frac {mathrm {d} z}{mathrm {d}t})^{2}}mathrm {d} t. }
L_{0}=int _{0}^{x_{0}} {{sqrt {1+{frac {9a^{2}}}x}};\mathrm {d} x={{frac {4}{9a^{2}}int _{0}^{{frac {9a^{2}}{4}x_{0}} {{sqrt {1+u}}; \mathrm {d} u={frac {8}{27a^{2}}left[(1+u)^{frac {3}{2}}right]_{0}^{{frac {9a^{2}{4}x_{0}={frac {(4+9a^{2}x_{0})^{frac {3}{2}-8}{27a^{2}}. }
{\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} \theta }}=a(1-\cos \theta ),\ {\frac {\mathrm {d} y}{\mathrm {d} \{\i}=a\i}sin \i} {\i}quad {\i}quad {\i}quad {\i}quad {\i}quad} izquierda({\frac {\mathrm {d} x}{\i}d} \i}derecha)^{2}+ izquierda({\frac {\mathrm {d} y}{\i}queda}{\i}derecha)^{2}=a^{2}(2- 2\cos(\theta ))=4a^{2} {left(1-\cos ^2}{frac {\theta }{2}\right)=4a^{2} {sin ^{2}{frac {\theta }{2}. }
Cómo calcular la longitud de un arco de círculo pdf
Un sector del círculo (también Kreisausschnitt) en geometría es el área parcial de un área circular delimitada por un arco y dos rayos circulares (en contraposición a un “segmento del círculo” delimitado por un arco y una cuerda).
Si seleccionas dos puntos de una línea circular y los conectas con el centro del círculo, obtendrás una sección del círculo. El área de la sección del círculo Aα (también llamada sector del círculo) está determinada por el tamaño del ángulo en el centro.
Se aplica lo siguiente: A : alfa = (pi * r²) : 360 °. Entonces A = (pi * r²) (alfa / 360 °). La tienda se da en radianes, las fórmulas se simplifican. Se aplica lo siguiente: b: alfa = (2pi * r) 2pi rad).
En un arco circular se aplican las siguientes fórmulas: Si el ángulo es alfa, el área es A = pi * r² * (Alfa / 360) y la longitud del arco (Longitud del arco parcial) b = pi * r² * (Alfa / 360).